matlab绘制"水花号"水线和计算浮心

project
2.5k words

Night 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
x = [36, 72, 108, 144, 180, 216, 252, 288, 324, 360, 396];
y_data = [
    25, 55.375, 71.25, 79.25, 83.75, 82.75, 81.25, 79, 74, 67.5, 61.375;    % 12Ab
    20, 52.5, 69.75, 78, 82.75, 82.25, 81, 78.75, 72.5, 65.875, 58.625;     % 6Ab
    13.75, 48.5, 66.25, 75.875, 80.75, 82, 80.75, 77.5, 72, 63, 45.5;       % DWL
    7.5, 41.5, 61.25, 72.625, 77.5, 79.25, 77.875, 73, 65.5, 50, 11.5;      % 6B
    0, 32.375, 52.25, 64.125, 71.125, 73.25, 70, 63.5, 49.5, 24.875, 0;     % 12B
    0, 20.5, 39.5, 51.25, 57.75, 59, 66.5, 45, 29, 10.5, 0;                 % 18B
    0, 9.75, 24.25, 33.5, 39.5, 40.75, 24.25, 27.5, 15.5, 6.5, 0;           % 24B
    0, 0, 6.25, 13.25, 18.75, 21.5, 19.25, 14.75, 8.75, 4.5, 0              % 30B
];

labels = ["12Ab", "6Ab", "DWL", "6B", "12B", "18B", "24B", "30B"];
colors = ["#054A91", "#3E7CB1", "#81A4CD", "#DBE4EE", "#B8D8D8", "#7CAFC4", "#90E0EF", "#CAF0F8"]; % 指定颜色

x_ = x(1):10:x(end);

figure;
hold on;
for i = 1:size(y_data, 1)
    p = polyfit(x, y_data(i,:), 2);
    y_ = polyval(p, x_);
    plot(x_, y_, 'LineWidth', 2, 'DisplayName', labels(i), 'Color', colors(i));
end
legend;
grid on;
xlabel('X-axis');
ylabel('Y-axis');
hold off;

Night 4: Computational COM and COB

(1)

直尺一维模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
%定义直尺属性
ruler.length = 30;   % 长度(cm)
ruler.weight = 25;   % 重量(g)

mesh.dx = 0.1;  % 定义模拟中每个小格(cell)的间距为0.1厘米    
mesh.xs = 0:mesh.dx:ruler.length;   % 创建一个从0到直尺长度的坐标数组，表示每个小格的位置，步长为mesh.dx。

ruler.density = ruler.weight/numel(mesh.xs);    % 通过直尺的总重量除以小格的总数(numel(mesh.xs))来计算每个小格的平均密度(质量)，单位为g/cell。

masses = ones(size(mesh.xs))*ruler.density;     % 创建一个与mesh.xs同样大小的数组，其中每个元素的值都是小格的密度，即每个小格的质量。
M = sum(masses);    

COM = centerOfMass(masses,mesh);

增添砝码

1
2
3
4
5
6
7
8
9
10
11
mass = 100;    % g
position = 3;  % cm
masses = addMass(mass,position,masses,mesh);

% 可修改参数
masses = addMass(50,10,masses,mesh);
masses = addMass(10,20,masses,mesh);
masses = addMass(5 ,5 ,masses,mesh);

COM_update = centerOfMass(masses, mesh); 
COM_update

亚克力板二维模拟

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
plate.length = 30;   % cm
plate.width = 30;     % cm
plate.weight = 77;   % g

clear mesh
% 模拟中每个cell在x轴y轴方向的间距均为0.1厘米，表示模拟的精度。
mesh.dx = 0.1;
mesh.dy = 0.1;
mesh.xs = 0:mesh.dx:plate.length;
mesh.ys = 0:mesh.dy:plate.width;

[mesh.xgrid, mesh.ygrid] = meshgrid(mesh.xs,mesh.ys); %生成二维网格，储存坐标

plate.density = plate.weight/numel(mesh.xgrid); 
masses_2D = plate.density * ones(size(mesh.xgrid));

M_2Dplate = matrixSum(masses_2D);

COM_2D = centerOfMass2(masses_2D, mesh);

COM_2D

[abc,index_z]=min(Z);
position_02=[Y(index_z),abc];
masses = addMass2(0.5,position_02,masses,mesh);  
COM_weight2 = centerOfMass2(masses, mesh);

增添砝码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
weight_2D = 100; %g
position_2D = [0.3,0.3]; %cm

masses_2D = Addmass_2D(weight_2D, position_2D, masses_2D, mesh);
masses_2D = Addmass_2D(50, [10,20], masses_2D, mesh);
masses_2D = Addmass_2D(20, [5,10], masses_2D, mesh);
masses_2D = Addmass_2D(10, [20,5], masses_2D, mesh);

new_weight = matrixSum(masses_2D);

COM2D_update_x = matrixSum(masses_2D.*mesh.xgrid)/new_weight;
COM2D_update_y = matrixSum(masses_2D.*mesh.ygrid)/new_weight;

COM2D_update = [COM2D_update_x, COM2D_update_y];

COM2D_update

(2)

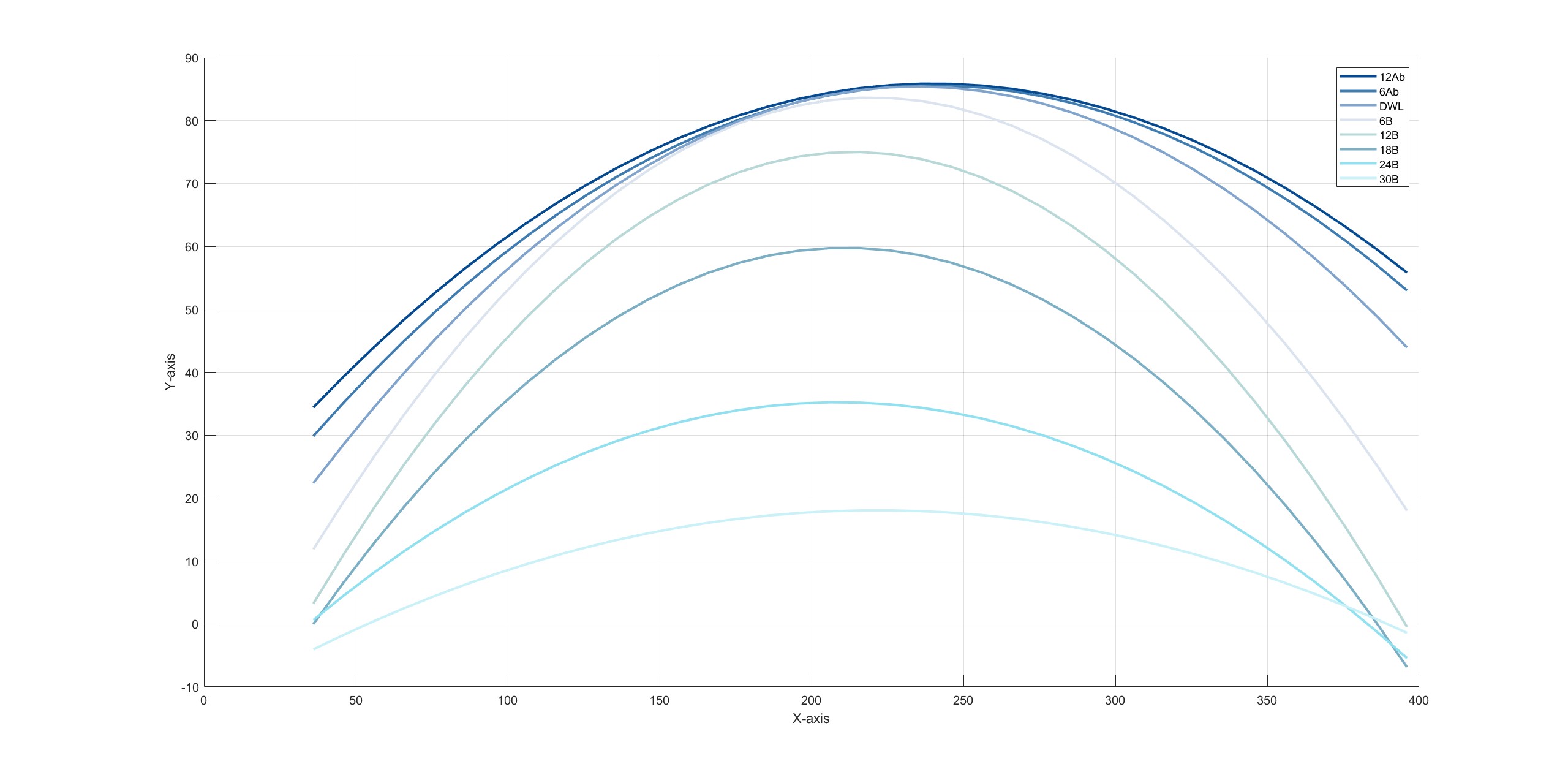
建立the spray三维曲面

最终效果：

安装并使用cftool，导入xyz数据集。采用Polynomial多项式拟合，x、y均为三次方。
其他拟合方式（非最终方案）效果如下：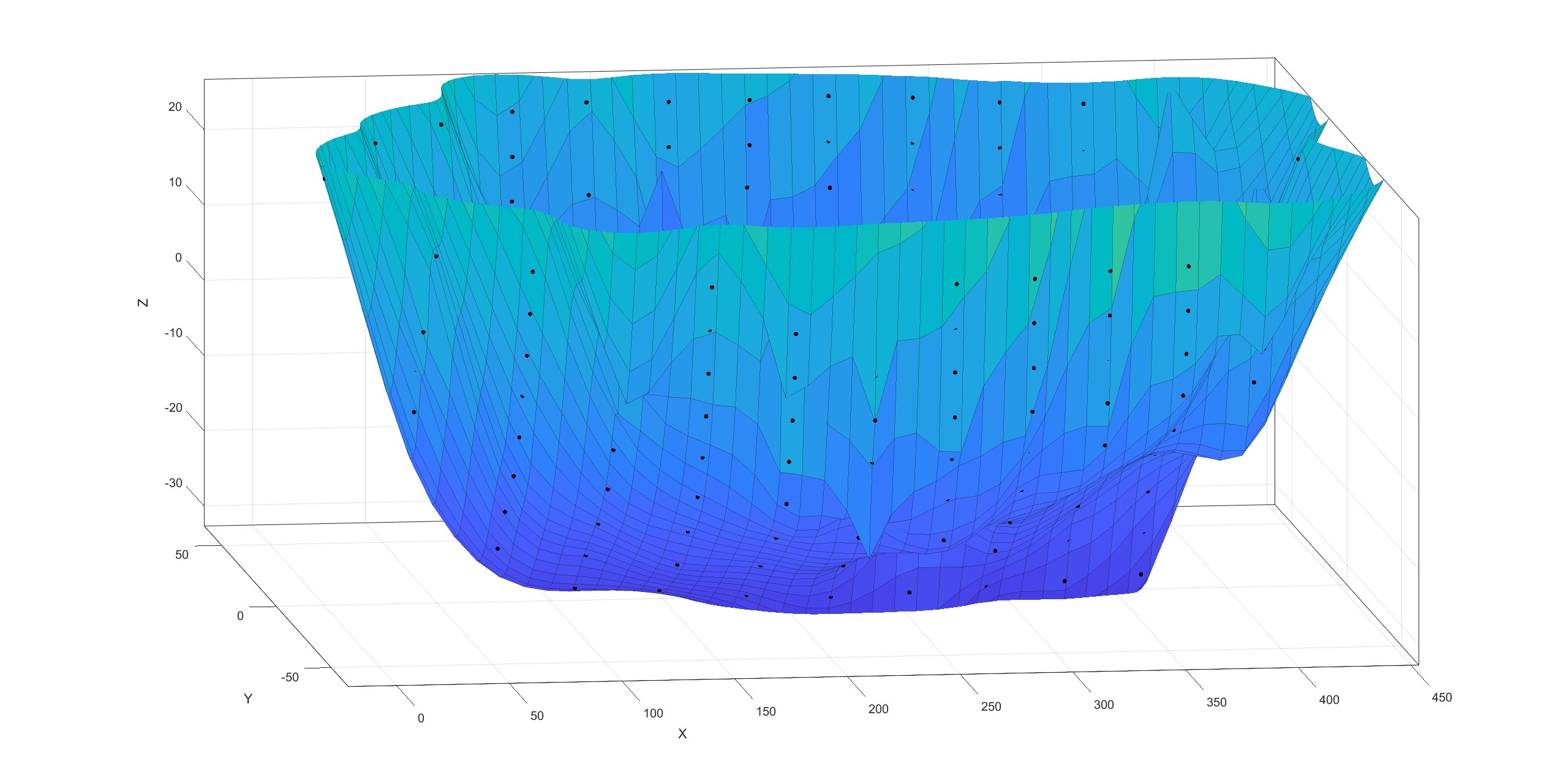

插值，薄板样条Thin Plate Spline

扩充点集，griddata拟合。

1
2
3
4
5
6
7
8
X = [ 0.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 432.000000 ];
Y = [ 0.000000 -27.750000 -27.750000 -17.000000 -16.000000 -9.750000 -7.500000 7.500000 9.750000 16.000000 17.000000 27.750000 27.750000 -41.750000 -41.750000 -39.375000 -36.500000 -32.500000 -29.500000 -24.375000 -16.500000 -9.750000 9.750000 16.500000 24.375000 29.500000 32.500000 36.500000 39.375000 41.750000 41.750000 -51.250000 -50.875000 -50.875000 -49.750000 -46.250000 -41.250000 -36.250000 -27.500000 -16.250000 -6.250000 6.250000 16.250000 27.500000 36.250000 41.250000 46.250000 49.750000 50.875000 50.875000 51.250000 -57.250000 -57.250000 -55.250000 -54.000000 -51.875000 -48.625000 -44.125000 -35.250000 -25.500000 -9.250000 9.250000 25.500000 35.250000 44.125000 48.625000 51.875000 54.000000 55.250000 57.250000 57.250000 -59.750000 -58.750000 -56.750000 -56.250000 -56.250000 -53.500000 -51.125000 -41.750000 -27.500000 -14.750000 14.750000 27.500000 41.750000 51.125000 53.500000 56.250000 56.250000 56.750000 58.750000 59.750000 -58.750000 -58.250000 -58.000000 -56.500000 -56.500000 -55.250000 -49.250000 -43.000000 -28.750000 -17.500000 17.500000 28.750000 43.000000 49.250000 55.250000 56.500000 56.500000 58.000000 58.250000 58.750000 -58.500000 -58.500000 -57.250000 -57.000000 -56.750000 -53.875000 -50.000000 -46.500000 -16.250000 -15.250000 15.250000 16.250000 46.500000 50.000000 53.875000 56.750000 57.000000 57.250000 58.500000 58.500000 -55.750000 -55.750000 -55.000000 -54.750000 -53.500000 -49.000000 -43.500000 -33.000000 -19.500000 -10.750000 10.750000 19.500000 33.000000 43.500000 49.000000 53.500000 54.750000 55.000000 55.750000 55.750000 -50.500000 -50.500000 -50.000000 -48.500000 -48.000000 -45.500000 -33.500000 -21.000000 -11.500000 -8.750000 8.750000 11.500000 21.000000 33.500000 45.500000 48.000000 48.500000 50.000000 50.500000 50.500000 -48.000000 -48.000000 -47.500000 -45.875000 -43.000000 -34.000000 -16.875000 -10.500000 -6.500000 -4.500000 4.500000 6.500000 10.500000 16.875000 34.000000 43.000000 45.875000 47.500000 48.000000 48.000000 -42.625000 -41.375000 -41.000000 -41.000000 -33.500000 -11.500000 11.500000 33.500000 41.000000 41.000000 41.375000 42.625000 0.000000 ];
Z = [ 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 12.000000 18.000000 24.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 18.000000 24.000000 12.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 12.000000 6.000000 0.000000 24.000000 18.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 18.000000 24.000000 0.000000 6.000000 12.000000 12.000000 6.000000 0.000000 24.000000 18.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 18.000000 24.000000 0.000000 6.000000 12.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 6.000000 12.000000 24.000000 18.000000 0.000000 -6.000000 -6.000000 0.000000 24.000000 18.000000 12.000000 6.000000 24.000000 ];
[Xi,Yi]=meshgrid(0:3:3000,-500:1:500);
Zi=griddata(X,Y,Z, Xi,Yi);
surf(Xi,Yi,Zi);
shading flat;
axis('equal');

(3)

计算the spray浮心

分析：船舶的浮心就是它排开水的部分的水的质心。
故沿x轴方向对船舶切片，计算切片的质心和浮心，最终可得整个船体的质心和浮心。
假设：船体为实心，且质量均匀分布

根据以上线性拟合结果得到拟合的线性模型方程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
线性模型 Poly33:
     f(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p30*x^3 + p21*x^2*y 
                    + p12*x*y^2 + p03*y^3
系数(置信边界为 95%):
       p00 =       24.74  (18.55, 30.93)
       p10 =     -0.7374  (-0.8701, -0.6048)
       p01 =  -1.632e-16  (-0.1365, 0.1365)
       p20 =    0.002366  (0.001669, 0.003062)
       p11 =   8.283e-19  (-0.001667, 0.001667)
       p02 =     0.01779  (0.01487, 0.02072)
       p30 =  -1.795e-06  (-2.821e-06, -7.681e-07)
       p21 =  -1.425e-21  (-3.618e-06, 3.618e-06)
       p12 =  -1.137e-05  (-2.312e-05, 3.759e-07)
       p03 =   2.422e-20  (-3.92e-05, 3.92e-05)

（数据经统一单位、处理后得出）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
X = [ 0.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 36.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 72.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 108.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 144.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 180.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 216.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 252.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 288.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 324.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 360.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 396.000000 432.000000 ];
Y = [ 0.000000 -27.750000 -27.750000 -17.000000 -16.000000 -9.750000 -7.500000 7.500000 9.750000 16.000000 17.000000 27.750000 27.750000 -41.750000 -41.750000 -39.375000 -36.500000 -32.500000 -29.500000 -24.375000 -16.500000 -9.750000 9.750000 16.500000 24.375000 29.500000 32.500000 36.500000 39.375000 41.750000 41.750000 -51.250000 -50.875000 -50.875000 -49.750000 -46.250000 -41.250000 -36.250000 -27.500000 -16.250000 -6.250000 6.250000 16.250000 27.500000 36.250000 41.250000 46.250000 49.750000 50.875000 50.875000 51.250000 -57.250000 -57.250000 -55.250000 -54.000000 -51.875000 -48.625000 -44.125000 -35.250000 -25.500000 -9.250000 9.250000 25.500000 35.250000 44.125000 48.625000 51.875000 54.000000 55.250000 57.250000 57.250000 -59.750000 -58.750000 -56.750000 -56.250000 -56.250000 -53.500000 -51.125000 -41.750000 -27.500000 -14.750000 14.750000 27.500000 41.750000 51.125000 53.500000 56.250000 56.250000 56.750000 58.750000 59.750000 -58.750000 -58.250000 -58.000000 -56.500000 -56.500000 -55.250000 -49.250000 -43.000000 -28.750000 -17.500000 17.500000 28.750000 43.000000 49.250000 55.250000 56.500000 56.500000 58.000000 58.250000 58.750000 -58.500000 -58.500000 -57.250000 -57.000000 -56.750000 -53.875000 -50.000000 -46.500000 -16.250000 -15.250000 15.250000 16.250000 46.500000 50.000000 53.875000 56.750000 57.000000 57.250000 58.500000 58.500000 -55.750000 -55.750000 -55.000000 -54.750000 -53.500000 -49.000000 -43.500000 -33.000000 -19.500000 -10.750000 10.750000 19.500000 33.000000 43.500000 49.000000 53.500000 54.750000 55.000000 55.750000 55.750000 -50.500000 -50.500000 -50.000000 -48.500000 -48.000000 -45.500000 -33.500000 -21.000000 -11.500000 -8.750000 8.750000 11.500000 21.000000 33.500000 45.500000 48.000000 48.500000 50.000000 50.500000 50.500000 -48.000000 -48.000000 -47.500000 -45.875000 -43.000000 -34.000000 -16.875000 -10.500000 -6.500000 -4.500000 4.500000 6.500000 10.500000 16.875000 34.000000 43.000000 45.875000 47.500000 48.000000 48.000000 -42.625000 -41.375000 -41.000000 -41.000000 -33.500000 -11.500000 11.500000 33.500000 41.000000 41.000000 41.375000 42.625000 0.000000 ];
Z = [ 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 12.000000 18.000000 24.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 18.000000 24.000000 12.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 12.000000 6.000000 0.000000 24.000000 18.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 18.000000 24.000000 0.000000 6.000000 12.000000 12.000000 6.000000 0.000000 24.000000 18.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 18.000000 24.000000 0.000000 6.000000 12.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 18.000000 24.000000 24.000000 18.000000 12.000000 6.000000 0.000000 -6.000000 -12.000000 -18.000000 -24.000000 -30.000000 -30.000000 -24.000000 -18.000000 -12.000000 -6.000000 0.000000 6.000000 12.000000 24.000000 18.000000 6.000000 12.000000 24.000000 18.000000 0.000000 -6.000000 -6.000000 0.000000 24.000000 18.000000 12.000000 6.000000 24.000000 ];

boat.L = 400;          %船的长度
boat.W = 100;          %船的宽度
boat.HB = boat.W / 2;  %船的半宽
boat.D = 60;           %船的深度
boat.HD = boat.D / 2;  %船的半宽

max_area = boat.D * boat.W              %沿X轴的切面（Y_Z平面切面）的最大面积
max_volume = max_area * boat.L          %立方体的体积
density_water = 28.312;                 %水的密度 （Kg/立方英尺）
max_mass = max_volume * density_water   %排开水的最大质量

dy = 1;   % meters（微元_Y轴）
dz = 1;   % meters（微元_X轴）

mesh.ys = -boat.HB:dy:boat.HB;  % meters  Y轴切片
mesh.zs = -boat.HD:dz:boat.HD;  % meters  Z轴切片

[mesh.ygrid,mesh.zgrid] = meshgrid(mesh.ys,mesh.zs);    %yz平面

total_area = boat.W * boat.D
mesh.dA = total_area / numel(mesh.ygrid)  %微元面积

ZMass=[];
XMass=[];
YMass=[];
MMass=[];   %每个浮心点的权重（质量）
tot_mass=0; %总质量

for i=2 : 11   %对每个x积分
    ZZ=[];  %记录该X下的Z轴坐标
    for j=1 : 101   %讨论y从[-60,60]
        t=caculate(i*36,mesh.ys(1,j));
        ZZ=[ZZ t];
    end
    y = mesh.ys;
    figure(i);  %绘制不同的图
    
    hull = mesh.zgrid > ZZ  %在所计算的Z的值之上的就是船的截面
    redmap = [1,1,1;1,0,0];
    colormap(redmap);
    image(mesh.ys,mesh.zs,flipud(hull),'AlphaData',0.5);
    
    %描述水线 y=kx+d
    d = 0.05; 
    theta = 10;
    y = mesh.ys;
    z = tand(theta) .* y + d;   %每个水线对应的方程
    
   
    water = mesh.zgrid < z;
    bluemap = [1,1,1; 0,0,1];
    plotMatrix(water,mesh,bluemap);
    %计算水线与切面的公共面积
    
    sub_region = hull & water;
    purplemap = [1,1,1; 1,0,1];
    plotMatrix(sub_region,mesh,purplemap);
    
    %计算浮心2D
    COB = centerOfMass2(sub_region,mesh);
    ZMass=[ZMass COB(1,1)];
    YMass=[YMass COB(1,2)];
    XMass=[XMass (i-0.5)*36];
    MMass=[MMass matrixSum(sub_region)];
    tot_mass=tot_mass+matrixSum(sub_region);
end
ANS=centerOfMass3(XMass,YMass,ZMass,MMass,tot_mass);%计算三维浮心
ANS

(3)

反思和总结

  • 建立更全面的模型，考虑船体材料密度差异和电力推动装置、配重分布等问题。
  • 增加切片数量和考虑更多的拟合方案，增加计算的精度。
Comments